Hasse diagram

English: A Hasse diagram is a graphical representation of a partially ordered set.

Misc.

Subsets of a 2-element set	Subsets of a 3-element set		Divisors of 60 ordered by divisibility		Non-negative integers ordered by divisibility
Young–Fibonacci lattice	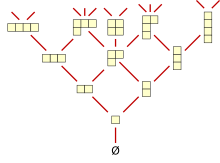Young's lattice		Left: Divisors of 120 ordered by divisibility (Birkhoff's representation theorem)
Associahedron of order 4		Permutohedron of order 4		Lattice of regular bands
Free distributive lattices of monotonic Boolean functions		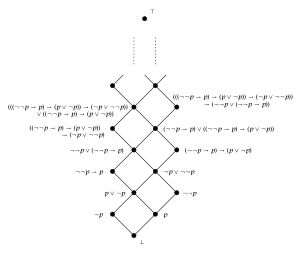Rieger–Nishimura lattice (free Heyting algebra over one generator)		Types of quadrilaterals

Subsets of a 4-element set:

Emphasis on two cubes	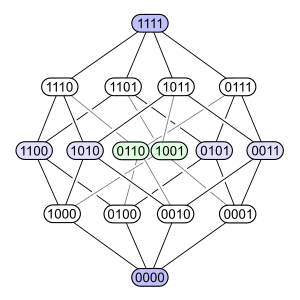Rhombic dodecahedral parallel projection of the tesseract	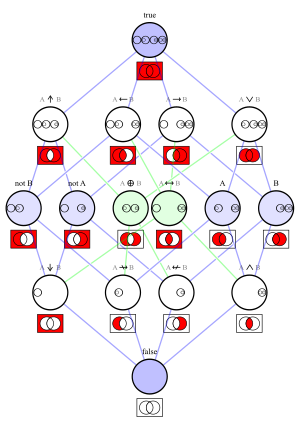Logical connectives
Emphasis on all eight cubes	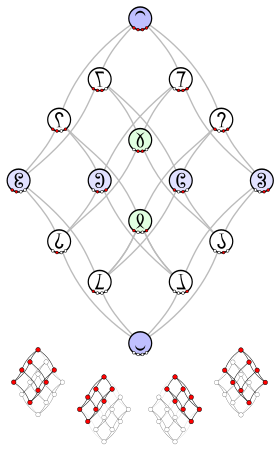4x4 matrix	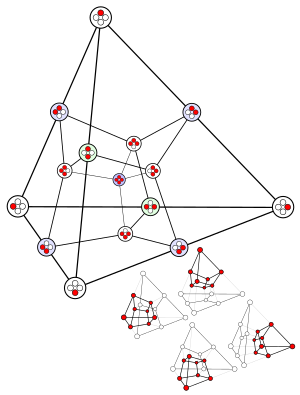Tetrahedral central projection of the tesseract Not a Hasse diagram, but similar: Highest element in center; lower elements farer away from center; lowest element not shown

Partitions of a 4-element set ordered by refinement:

		Only the 14 noncrossing partitions (This diagram is also vertically symmetric.)
Emphasis on sublattice	Emphasis on symmetry	Emphasis on number of elements per rank

Dihedral group Dih₄	Z₂³	Z₂⁴ (rank expressed by background color, not by position)
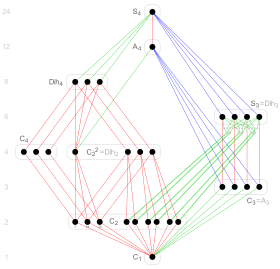30 subgroups of S₄	9 types of subgroups of S₄	25 types of subgroups of the S₄ × C₂